Découvrez Comment Trouver L’équation De La Tangente À Une Courbe
Apprenez À Trouver L’équation De La Tangente D’une Courbe À Un Point Donné. Maîtrisez Les Étapes Pour Rencontrer L’équation De La Droite Tangente Facilement.
**applications Pratiques Des Tangentes Dans La Géométrie**
- Les Bases Des Tangentes Et Leur Importance
- Applications Pratiques Dans Le Design Architectural
- La Tangente En Physique : Concepts Clés
- Utilisation Des Tangentes En Informatique Graphique
- Tangentes Et Optimisation : Une Approche Mathématique
- Exemples Célèbres : Tangentes Dans L’art Et La Nature
Les Bases Des Tangentes Et Leur Importance
Les tangentes représentent un concept fondamental en géométrie, servant de points de contact entre une courbe et une ligne droite. Leur vitalité dans les mathématiques réside non seulement dans leur capacité à simplifier des problèmes complexes, mais aussi à offrir une approche visuelle pour comprendre les changements instantanés. Imaginez une route sinueuse ; la tangente à un point donné représente la direction dans laquelle vous allez instantanément, comme un conducteur qui fait une virage. Cela démontre comment les tangentes sont liées à la notion de dérivée, une idée qui est devenue la pierre angulaire du calcul.
Dans le monde du design architectural, les tangentes sont omniprésentes, influençant la conception de structures élégantes et fonctionnelles. Les architectes les utilisent pour analyser les courbes et les angles, permettant ainsi de créer des formes harmonieuses qui s’intègrent parfaitement dans leur environnement. Ces principes peuvent être comparés à la création d’une recette de médicament; comprendre comment les ingrédients interagissent (dans ce cas, les lignes et les courbes) peut mener à une belle harmonie. La précision avec laquelle ces tangentes sont utilisées assure que chaque élément d’une structure est en équilibre.
De plus, la capacité des tangentes à représenter des moments critiques dans divers domaines fait d’elles un outil inestimable. Que ce soit pour dessiner le chemin d’une balle projetée ou pour optimiser des équations en physique, les tangentes facilitent des calculs essentiels qui se produisent souvent “stat” dans les applications pratiques. Ainsi, comprendre et maîtriser ce concept est non seulement nécessaire pour les mathématiciens, mais aussi pour les professionnels impliqués dans la technologie, l’architecture et même l’art.
| Concept | Application | Importance |
|---|---|---|
| Tangente | Analyse de courbes | Simplification de problèmes |
| Design architectural | Création de structures | Harmonie et équilibre |
| Calculs de dérivées | Optimisation en physique | Representation de changements instantanés |

Applications Pratiques Dans Le Design Architectural
Dans le design architectural, les tangentes jouent un rôle essentiel, non seulement en termes d’esthétique, mais aussi de structure. Lorsqu’un architecte souhaite intégrer des courbes fluides dans ses plans, il doit en premier lieu s’assurer que chaque courbe soit en harmonie avec les lignes droites qui l’entourent. C’est à ce moment-là que la notion de tangente devient cruciale. En analysant une forme donnée, un professionnel peut facilement déterminer comment la tangente s’ajuste à la courbe à un point spécifique. Cette compétences est comparable à l’importance d’un script bien écrit dans une prescription : elle définit la direction à suivre pour atteindre le résultat désiré. En utilisant la méthode pour encontre équation reta tangente curva ponto dado, les architectes peuvent préjuger des contraintes techniques et optimiser les espaces, créant des environnements non seulement fonctionnels mais aussi esthétiquement plaisants.
Par ailleurs, dans la construction de structures telles que des arches ou des ponts, les propriétés des tangentes permettent d’atteindre un équilibre délicat entre force et légèreté. En effet, le choix des angles et des courbes peut déterminer le succès d’un projet tout entier. Les tangentes aident également à minimiser les défauts tout en veillant à ce que la sécurité soit maintenue, un concept similaire à celui de la gestion des médicaments où chaque composant doit être soigneusement dosé. Ainsi, l’art de curviligne dans l’architecture, guidé par les principes geometrie des tangentes, peut certainement transformer des idées en réalisations tangibles et impressionnantes. Les architectes s’attachent à un design intuitif qui capte l’œil tout en respectant les standards techniques nécessaires.
La Tangente En Physique : Concepts Clés
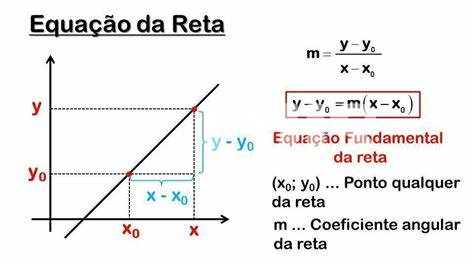
Dans le domaine de la physique, l’application des tangentes revêt une importance capitale, notamment lorsqu’il s’agit de comprendre le comportement des objets en mouvement. La notion de pente d’une tangente à une courbe permet de déterminer la vitesse instantanée d’un objet à un moment donné. Par exemple, si nous avons une courbe représentant la position d’un corps en mouvement, la rencontre entre l’équation d’une droite tangente et la courbe au point donné nous offre une perspective sur la dynamique de l’objet. Ce concept peut être simplifié par l’analogie avec une prescription médicale : la tangente représente les instructions sur un traitement à suivre, où chaque point sur la courbe peut être vu comme un moment de la progression du patient. Ainsi, la compréhension des tangentes devient essentielle pour prédire les variations et les comportements des systèmes physiques en temps réel.
En outre, les applications des tangentes se retrouvent souvent dans des phénomènes naturels, tels que la propagation des ondes ou la description des champs de force. Par exemple, les champs gravitationnels peuvent être analysés à travers les tangentes aux courbes représentant les trajectoires des masses. Ce lien entre géométrie et physique démontre que, tout comme un pharm Tech s’assure que chaque médicament est correctement administré, les tangentes permettent aux physiciens de “prescrire” des solutions pour des problèmes complexes. De plus, ces concepts sont fondamentalement interconnectés avec des méthodes numériques sophistiquées, souvent utilisées dans des simulations, ce qui souligne l’importance d’adopter une approche systématique dans l’étude de la physique moderne.

Utilisation Des Tangentes En Informatique Graphique
Dans l’univers dynamique de l’informatique graphique, les tangentes jouent un rôle essentiel pour représenter la fluidité des formes et la précision des contours. Lorsqu’un concepteur souhaite créer une animation ou un modèle 3D, il devra souvent s’en référer à l’équation de la droite tangente à une courbe à un point donné. Cela permet non seulement d’assurer que les mouvements paraissent naturels, mais aussi d’optimiser les calculs, rendant le rendu visuel plus efficace et rapide, ce qui est crucial pour des applications en temps réel.
Les applications pratiques de cette notion vont bien au-delà de l’esthétique. Par exemple, dans la conception de jeux vidéo, les tangentes aident à déterminer les trajets des objets en mouvement. En utilisant des algorithmes basés sur ces concepts, les développeurs peuvent modéliser les réactions physiques des personnages et des environnements de manière réaliste. Cette approche n’est pas seulement un simple embellissement; elle contribue à une expérience immersive qui captive l’utilisateur.
L’intégration des tangentes dans le traitement graphique ne se limite pas à des calculs techniques. Elle joue également un rôle dans des domaines comme la vision par ordinateur, où il est nécessaire de détecter des bords et des contours avec précision. Ces techniques facilitent la reconnaissance d’objets, ce qui a des applications dans les véhicules autonomes et les systèmes de surveillance. Ainsi, la compréhension et l’application des tangentes dans ces contextes sont devenus une compétence indispensable pour les professionnels du secteur technologique.
Tangentes Et Optimisation : Une Approche Mathématique
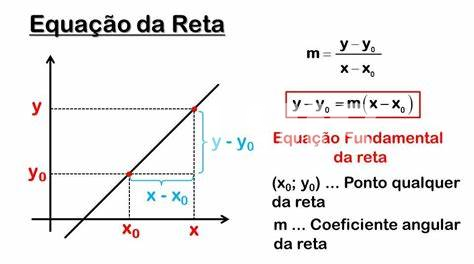
L’optimisation mathématique utilise de nombreux outils pour résoudre des problèmes complexes, et l’un d’eux est l’étude des tangentes. En effet, la rencontre entre une équation droite, la tangente, et la courbe à un point donné joue un rôle crucial dans la détermination des valeurs maximales et minimales de fonctions. Lorsque nous voulons maximiser ou minimiser une fonction, la pente de la tangente devient une référence essentielle. À partir du point donné sur la courbe, si nous faisons des petits ajustements, nous pouvons évaluer comment ces changements affectent le résultat global, ce qui nous permet d’évaluer les points critiques, également appelés points stationnaires.
Prenons l’exemple d’une fonction représentant le coût de production d’un bien. Supposons que nous souhaitions minimiser ce coût tout en respectant certaines contraintes. L’équation qui définit la tangente à la courbe de coût peut nous indiquer comment le coût réagit aux variations de production. Au moment de l’optimisation, cet instantané devient inestimable pour les gestionnaires cherchant à établir un comp. Dans cette démarche, les dérivées jouent leur rôle, montrant que la tangente n’est pas seulement une ligne ; elle est le reflet de la façon dont les variables interagissent dans un espace multidimensionnel.
Il existe aussi des approches où un point de départ est essentiel pour parcourir une courbe graphique, à la manière d’un script illustrant des décisions financières. Ainsi, en utilisant une méthode d’optimisation appelée “méthode des gradients”, nous pouvons naviguer plus efficacement sur les pentes. En représentant les équations de manière graphique avec les tangentes, on peut non seulement repérer des solutions potentielles, mais également déterminer la direction à prendre. Ces éléments aboutissent à des résultats plus raffinés et pertinents dans la modélisation des systèmes réels.
| Aspect | Description |
|---|---|
| Pente de la Tangente | Représente le taux de variation d’une fonction à un point donné. |
| Point Stationnaire | Lieu où la dérivée égale zéro, indiquant un minimum ou un maximum potentiel. |
| Optimisation | Processus pour trouver les meilleures solutions à un problème donné. |
Exemples Célèbres : Tangentes Dans L’art Et La Nature
Dans l’art, les tangentes jouent un rôle clé, notamment dans la création de compositions dynamiques et équilibrées. Par exemple, les célèbres œuvres de l’artiste italien Pablo Picasso illustrent comment des formes géométriques, lorsqu’elles s’entrelacent, peuvent engendrer des tangentes invisibles qui dirigent le regard du spectateur. Ces lignes tangentielles, bien que souvent indétectables, créent une sensation de mouvement et de fluidité, captivant notre attention. De plus, dans la nature, le phénomène des anticyclones et des tornades montre comment les tangentes influencent les cycles naturels. Cette relation s’observe par les courants d’air qui, formant des tangentes à zemigrerence avec le sol, créent des vortex. Ce lien entre art et nature souligne l’harmonie évidente qui existe dans les structures fondamentales de notre environnement.
En explorant ces concepts, on peut également faire un parallèle avec le monde de la santé ou de la pharmacie, où la précision est de mise. Parfois, une simple tangente d’un médicament peut transformer un traitement. Lorsqu’on considère la manière dont les prescriptions sont délivrées et comment les professionnels de la santé naviguent à travers des processus complexes, les analogies avec l’art et la nature deviennent encore plus pertinentes. Les bonnes pratiques, tout comme dans l’art d’utiliser les tangentes, exigent une excellente attention aux détails, un timing impeccable, et une capacité à interpréter des données complexes pour offrir la meilleure solution possible.